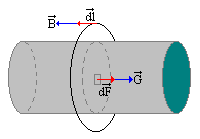
Por un cable conductor pasa una densidad de corriente G, entonces, la intensidad de corriente eléctrica es
I = ò ò G.dF
La ley de Ampere puede escribirse como:

Por lo tanto


Con el teorema de Stokes se puede deducir que


por lo tanto

rot H = G (1)

Todo esto indica que en cada espacio donde existan densidades de corriente existen también rotacionales o remolinos del campo magnético.

Basándose en estas observaciones, es válido decir que no existen cargas magnéticas, pues, el campo magnético es generado por dipolos magnéticos y por lo tanto, su divergencia es nula.

div H = 0

por ser la inducción magnética un vector linealmente dependiente del campo magnético su divergencia también es nula:

div B = 0


El Potencial Vectorial Magnético libre de fuentes "A"

Dado que la divergencia del campo magnético es nula, es decir, el campo magnético no tiene fuentes, entonces, este se puede expresar como el rotacional de un campo vectorial libre de fuentes, en otras palabras, como el rotacional de un campo no gradiental.

div B = 0 Þ B = rot A Ù div A = 0 (2)

con (1):

G = rot H Þ m G = rot B

Con (2):

mG = rot rot A Þ mG = -D A (3)



El Potencial Escalar Magnético "Vm"

Supóngase el caso en el que el campo magnético es generado por la corriente que fluye a través de un inductor de espiras muy finas. El volumen encerrado por el inductor no contiene densidades de corriente, por lo tanto G = 0.