martes, 1 de diciembre de 2009
EXPOCICION
INTEGRANTES:
CASTRO CASTRO ENID YORMERI
PARRA LEON MARYEL
OBESO SOTO CECILIA
MONTOYA RUBIO JORGE LUIS
FELIX GALINDO GEOVANNY
En 1824 el ingeniero francés Sadi Carnot estudió la eficiencia de las diferentes máquinas térmicas que trabajan transfiriendo calor de una fuente de calor a otra y concluyó que las más eficientes son las que funcionan de manera reversible. Para ello diseñó una máquina térmica totalmente reversible que funciona entre dos fuentes de calor de temperaturas fijas. Esta máquina se conoce como la máquina de Carnot y su funcionamiento se llama el ciclo de Carnot.
El Ciclo llamado de Carnot es un ciclo reversible que consta de cuatro tramos: dos a temperatura constante (dos procesos isotérmicos), y otros dos sin absorción ni
cesión de calor (dos procesos adiabáticos). Es decir, se trata de una transformación bitérmica (entre dos temperaturas).tal como se muestra a continuación:
La máquina de Carnot puede pensarse como un cilindro con un pistón y una biela que convierte el movimiento lineal del pistón en movimiento circular. El cilindro contiene una cierta cantidad de un gas ideal y la máquina funciona intercambiando calor entre dos fuentes de temperaturas constantes T1 < T2. Las transferencias de calor entre las fuentes y el gas del cilindro se hace isotérmicamante, es decir, manteniendo la temperatura constante lo cual hace que esa parte del proceso sea reversible. El ciclo se completa con una expansión y una compresión adiabáticas, es decir, sin intercambio de calor, que son también procesos reversibles.
Como todos los procesos que tienen lugar en el ciclo ideal son reversibles, el ciclo puede invertirse. Entonces la máquina absorbe calor de la fuente fría y cede calor a la fuente caliente, teniendo que suministrar trabajo a la máquina. Si el objetivo de esta máquina es extraer calor de la fuente fría se denomina máquina frigorífica, y si es aportar calor a la fuente caliente bomba de calor.
La máquina de Carnot puede pensarse como un cilindro con un pistón y una biela que convierte el movimiento lineal del pistón en movimiento circular. El cilindro contiene una cierta cantidad de un gas ideal y la máquina funciona intercambiando calor entre dos fuentes de temperaturas constantes T1 < T2. Las transferencias de calor entre las fuentes y el gas del cilindro se hace isotérmicamante, es decir, manteniendo la temperatura constante lo cual hace que esa parte del proceso sea reversible. El ciclo se completa con una expansión y una compresión adiabáticas, es decir, sin intercambio de calor, que son también procesos reversibles.
Expansión isotérmica: (proceso 1 → 2 en el diagrama) Se parte de una situación en que el gas se encuentra al mínimo volumen del ciclo y a temperatura T1 de la fuente caliente. En este estado se transfiere calor al cilindro desde la fuente de temperatura T1, haciendo que el gas se expanda. Al expandirse, el gas tiende a enfriarse, pero absorbe calor de T1 y mantiene su temperatura constante. Al tratarse de un gas ideal, al no cambiar la temperatura tampoco lo hace su energía interna, y despreciando los cambios en la energía potencial y la cinética, a partir de la 1ª ley de la termodinámica vemos que todo el calor transferido es convertido en trabajo:
Expansión adiabática: (2 → 3) La expansión isoterma termina en un punto tal que el resto de la expansión pueda realizarse sin intercambio de calor. A partir de aquí el sistema se aísla térmicamente, con lo que no hay transferencia de calor con el exterior. Esta expansión adiabática hace que el gas se enfríe hasta alcanzar exactamente la temperatura T2 en el momento en que el gas alcanza su volumen máximo. Al enfriarse disminuye su energía interna, con lo que utilizando un razonamiento análogo al anterior proceso:
Compresión isoterma: (3 → 4) Se pone en contacto con el sistema la fuente de calor de temperatura T2 y el gas comienza a comprimirse, pero no aumenta su temperatura porque va cediendo calor a la fuente fría. Al no cambiar la temperatura tampoco lo hace la energía interna, y la cesión de calor implica que hay que hacer un trabajo sobre el sistema:
Compresión adiabática: (4 → 1) Aislado térmicamente, el sistema evoluciona comprimiéndose y aumentando su temperatura hasta el estado inicial. La energía interna aumenta y el calor es nulo, habiendo que comunicar un trabajo al sistema:
Este resultado es fundamental. Nos indica que el rendimiento de un Ciclo de Carnot depende exclusivamente de las temperaturas de los focos frío y caliente y no de las cantidades de calor transvasadas ni del tipo de sustancia con la que funciona el ciclo.
Todos los Ciclos de Carnot, operando entre dos temperaturas dadas, tienen el mismo rendimiento.
•El ciclo completo • Variación de energía interna
•En un proceso cíclico reversible la variación de energía interna es cero • Trabajo
•Los trabajos en las transformaciones adiabáticas son iguales y opuestos. A partir de las ecuaciones de las dos adiabáticas, la relación entre los volúmenes de los vértices es , lo que nos conduce a la expresión final para el trabajo. • Calor En la isoterma T1 se absorbe calor Q>0 ya que vB>vA de modo que En la isoterma T2 se cede calor Q<0 ya que vD
ESCRITO EN CLASE
ESPECTRO ELECTROMAGNETICO:-ESTA FORMADO POR LOS SIGUIENTES TIPOS DE RAYOS:
RAYOS INFRAROJO: SON EMITIDOS POR CUALQUIER CUERPO QUE ESTE A UNA TEMPERATURA MAYOR QUE LOS O K, TAMBIEN SON CONOCIUDOS COMO RAYOS TERMICOS.UN EJEMPLO SON LOS RAYOS EMITIDOS POR EL SOL.
SON AQLUZ VISIBLE:UELLOS QUE PUEDEN SER PERCIBIDOS POR EL OJO HUMANO. ESTE TIPO DE RAYOS SON UNA PORCION DE LOS DISTINTOS RAYOS QUE CONFORMAN EL ESPECTRO ELECTROMAGNETICO.
RAYOS X: ESTE TIPO DE RAYO SE GENERA CUANDO UN HAS DE ELECTRONES QUE VIAJA A GRAN VELOCIDAD Y EN ALTO VASIO, SE FRENA BRUSCAMENTE AL CHOCAR CON UN OBSTACULO. ESTOS RAYIOS SON MUY PENETRANTES POR LO QUE SON EMPLEADOS PARA OBTENER RADIOGRAFIA.
- RAYOS ULTRA VIOLETA: ESTA TIPO DE RAYOS TAMBIEN SON CONOCIDOS COMO LUZ NEGRA, YA QUE EL OJO HUMANO NO LOS ADBIERTE, SOLO ALGUNOS INSECTOS LO PUEDEN DISTINGUIR.
ONDAS DE RADIO: SON LAS EMPLEADAS PARA TRANSMITIR SEÑALES A GRANDES DISTANCIA, ESTA SE CREAN POR ELECTRONES QUE OSCILAN EN UNA ANTENA.
RAYOS GAMMA: SON LOS PRODUCIDOS DURANTE LAS TRANSFORMACIONES NUCLEARES.
Problemas en clases
B=(N.M.I)/2r
B=(200)(4PIX210^-7(60)/2(30)
B=2.5132X10^-4 TESLAS
2.-LA INTENSIDAD DEL CAMPO MAGNETICO INDUCIDO EN EL CENTRTO DE UNA ESPIRA DE 20 CM. DE RADIO QUE SE ENCUENTRA EN AIRE Y POR LA CUAL CIRCULA UNA DINTENSIDAD DE CORRIENTE DE 26 PI A ES
:B= (M.I)2r
B= (4PIX10^-7)(25/PI)/ 2(20)
B=2.5X10^-5 TESLAS
3.- EL CAMPO MAGNETICO INDUCIDO POR UN SOLENOIDE DE 40 CM DE LONGITUD Y 500 VUELTAS QUE S ENCUNTRA RODIADO POR AIRE Y POR EL CUAL CIRCULA UNA CORRIENTE DE 200 A ES
:B= N.M.I/L
B= (500)(4PIX10^-7)(200)/(.40)
B= .3141 TESLAS
B= .PI TESLAS.
Hecho en clases
INDUCCION ELECTROMAGNETICA:EN EL AÑO DE 1831 EL CIENTIFICO INGLES MICHAEL FARADAY DESCUBRIO LAS CORRIENES ELECTRICAS ADUCIDAD APARTIR DE EXPERIMENTOS QUE REALIZO CON UNA BOBINA Y UN IMAN.LA INDUCCION ELECTROMAGNETICA DA COMO RESULTADO LA PRODUCCION DE UNA CORRIENTE INDUCIDA Y DE UNA FUERZA ELECTROMOTRIZ (FEM).
RELACION ENTRE EL CAMPO MAGNETICO Y EL CAMPO ELECTRICO:UN CAMPO MAGNETICO VARIABLE PRODUCE UN CAMPO ELECTRICO Y UN CAMPO ELECTRICO VARIABLE PRODUCE UN CAMPO ELECTRICO. LA MAGNITUD DE LA FUERZA QUE ACTUA SOBRE UNA CARGA Q QUE SE MUEVE CON UNA VELOCIDAD V, PRODUCIDA POR UN CAMPO ELECTRICO E , PERPENDICULAR TANTO A V Y A B. POR TANTO, LOS CAMPOS ELECTRICOS Y MAGNETICOS SE RELACIONAN DE LA SIGUIETE MANERA.
F=B.Q.V
Y
E=F/TE=B.V
DONDE:F= FUERZA SOBRE LA CARGA ELECTRICA
B=MAGNITUD DEL CAMPO ELECTRICO
Q= CARGA ELECTRICA
V= VELOCIDAD DE LA CARGA ELECTRICA
E= MMAGNITUD EEL CAMPO ELECTRICO
INDUCCION DE CAMPOS:CAMPO MAGNETICO INDUCIDO POR UN CONDUCTOR RECTO.LA MAGNITUD DEL CAMPO MAGNETICO B INDUCIDO POR UN CONDUCTOR RECTO, POR EL QUE CIRCULA UNA INTENSIDAD DE CORRIENTE Y UNA DETERMINADA DISTANCIA DE DEL CONDUCTOR, SE OBTIENE CON LA SIGUIENTE FORMULA:
B=M.I/2πD
DONDE:I=INTENSIDAD ( AMPERES)
D= DISTANCIA
B=MAGITUD DEL CAMPO MAGNETICO( TESLAS)
π=3.1416
-SI EL MEDIO QUE RODEA EL CONDUCTOR ES AIRE, ENTONCESM=M0=4πX10-7
CAMPO MAGNETICO INDUCIDO POR UNA ESPIRA:UNA ESPIRA SE OBTIENE AL DOBLAR EN FORMA CIRCULAR UN CONDUCTOR RECTO. LA INTENSIDAD DEL CAMPO MAGNETIO. B PRODUCIO POR LA ESPIRA DE RARIO R POR LA QUE CIRUCLA UNA CORRIENE ELECTRICA I ES:
B=M.I/2R
CAMPOR MAGNETICO PRODUCIDO POR UNA BOBINA:UNA BOBINA RESULTA DE ENRROLLAR UN ALAMBRE ENCIERTO NUMJERO DE VECES VUELTA, LA INTENSIDAD DE CORRIENE I SE OBTIENE DE LA SIGUEINTE FORMULA.
B=N.M.I/WR
CAMPO MAGNETICO PRODUCIDO POR UN SOLENOIDE:UN SOLENOIDE SE FORMA AL ENRROLLAR UN ALAMBRE EN FORMA ELICOIDAL. LA INTESIDAD DEL CAMPO MAGNEICO B PRODUCIDO POR UN SOLENOIDE DE N VUELTAS Y LONGITUD L, POR EL QUE CIRCULA UNA INTENSIDAD DE CORRIENTE L SE OBTIENE:
B=N.M.I/L
EJERCISIOS EN CLASE
4.-¿cual es al intencidad del campo elelctrico producido por una carga elelctrica de 3x10^-7 C a una distancia de dos metros de su centro?
k=9x10^9 nm^2/c^2
carga=3x10^-7 C
d=2m
I=?
E=K(Q)/D^2
E= (9X10^9) (3X10^-7)/(2)^2
E=675 N/C
5.-La intencidad del campo elelctrico en una cierta region es de 3x10^6 N/C. ¿cual es la magnitud de la carga que experimenta a una fuerza de 12 new.?
I=3X10^6 N/C
F=12 NEW
MAG= ?
F=ExQ
Q=F/E
Q=12N/3X10^6 = 0.000004
Q=4X10^-6
6.-Una carga de 5X10^-6 C se encuentra a 0.5 CM. de una carga de-3X10^-6 C.
¿cual es al magnitud d ela fuerza de atraccion entre las cargas?
Q1=5X10^-6
Q2= -3X10^-6 C
D=.5CM
E=(9X10^9)(5X10^-6)(-3X10^-6 C)/ (.005)2
E= 5400N
EJERCICIOS EN CLASES
2.-Tres resistencias de 6,3 y 4 OHM se conectan en paralelo y una corriente total de 30A se distribuye entre las tres.¿cual es al diferencia de potencial aplicada al circuito?

1/RT=1/6,1/3,1/4
CAMPO ELECTRICO
REGION DEL ESPACIO QUE REDEA A UNA CARGA ELECTRICA. LA MAGNITUD DEL CAMPO ELECTRICO PRODUCIDO POR UNA CAMPO DE FUERZA F, SOBRE UNA CARGA DE PRUEBA U SE OBTIENE:
1.- UNA CARGA DE (6X10)-6 C. SE INTRUDUCE A UNA REGION DONDE ACTUA UN CAMPO DE FUERZA .18N. CUAL ES LA INTENSIDAD DEL CAMPO ELECTRICO DE ESTAREGION?
E=F/Q .18/(6X10)-6 C.= 30000N/C
2.- EL CAMPO ELECTRICO UNA CIERTA REGION ES DE (5X10)20N/C. CUALCULA LA INTENSIDAD DE LA FUERZA QUE ACTUA SOBRE UN ELECTRON INVERSO EN ESTE CAMPO?
F= ((5X10)20N/C.)(1.6X10^19) =80N
3.- LA INTENSIDAD DE UNA CAPO ELECTRICO EN UNA CIERTA REGION ES DE 3X10^6 N/C. ¿CUAL ES LA MAGNITUD DE LA CARGA QUE EXPERIMENTA UNA FUERZA DE 12N?
Q=12/3X10^6=4X10^6
LEY DE OHM Y POTENCIAL ELECTRICO
LA INTENSIDAD DE CORRIENTE ELECTRICA QUE CIRCULA POR UN CONDUCTOR ES DIRECTAMENTE PROPORCIONAL AL VOLTAJE APLICADO A SUS ESTREMOS E INVERSAMENTE PROPORCIONAL A SU RESISTENCIA.
I=V/R
V=RI
R=V/I
lunes, 30 de noviembre de 2009
FLUJO MAGNETICO

Se si dibuja el resultado del experimento realizado y descrito en la leccion anterior, se obtiene la figura.
Las líneas a trazos indican el recorrido de las líneas de fuerza. Basta con dibujar algunas de ellas para representar el campo magnético.
Las líneas de fuerza no solo existen fuera del imán, si no que también recorren su interior. De hecho se deduce la siguiente regla:
“las líneas de fuerzas de un campo magnético son cerradas, todas las lineas de fuerzxa de un campo constituyen el flujo magnético”.
DENSIDAD DEL FLUJO MAGNÉTICO.
Las líneas que actúan entre dos imanes rectos alcanzan su valor máximo en los polos (repulsión o atracción), porque el flujo magnético tiene en ellos su densidad máxima.
La densidad del flujo magnético expresa el efecto del campo. También se denomina inducción magnética.
La densidad del flujo indica en valor de la intensidad del flujo magnético que atraviesa perpendicularmente la unidad de superficie (Cm2 o m2).
Para un campo magnético homogéneo resulta fácil calcular la densidad del flujo magnético:
Densidad del flujo es igual al Flujo magnético sobre la sección transversal del campo.
PROPIEDADES DE LOS IMANES.
Entre los materiales ferromagnéticos que son atraídos pos los imanes, figuran el hierro (acero o fundición de hierro), el níquel, el cobalto, determinadas aleaciones, como por ejemplo álnico (aluminio – níquel – cobalto, y óxidos mixtos sintetizados. (Ferritas).
Mediante un tratamiento especial pueden convertir las piezas de los materiales ferromagnéticos en imanes permanentes.
Los imanes más conocidos son los que tienen forma de barra o de herradura así como las agujas de las brújulas.
Todos los imanes tienen dos propiedades peculiares:
atraen el hierro y lo retienen (efecto fuerza).
se pueden mover libremente, se sitúan en dirección norte sur (efecto de orientación).
Este efecto de orientación o direccional se aplica en la brújula. Según su aguja, colocada de modo que pueda girar, se orienta en el campo magnético de la tierra de tal forma que siempre la misma punta (por regla general, de color azul) señala aproximadamente hacia el polo norte geográfico. Esta parte de la aguja se denomina polo norte y, en consecuencia, el extremo opuesto recibe el nombre de polo sur.
2.5.2 SATURACIÓN MAGNÉTICA Y MAGNETISMO REMANENTE.
Cuanto mayor sea el número de imágenes de imanes moleculares orientados en un material, tanto mas intenso será su efecto magnético. Si están ordenados todos los imanes moleculares, es imposible incrementar dicho efecto magnético. En el caso. El material esta magnéticamente saturado.
Después de imantado, el acero conserva bastante bien sus propiedades magnéticas solo un porcentaje reducido de los imanes moleculares vuelve a una posición desordenada después de suprimir el efecto magnetizante. La mayor parte de los imanes moleculares permanece orientada debido al rozamiento interno. Los materiales que tienen esta propiedad se denominan magnéticamente duros.
Materiales magnéticamente blandos son aquellos que pierden la mayor parte de su magnetismo al suprimir el efecto magnetizante. El rozamiento interno en dichos materiales es débil; los imanes moleculares se pueden ordenar con facilidad, pero también vuelven a fácilmente al estado desorden. Un material magnetizante blando es, por ejemplo, la chapa magnética. La propiedad indicada hace que los materiales magnéticamente blandos sean apropiados entre otros fines, pasa su empleo en transformadores.
El magnetismo que queda en un material después de su imantación se denomina magnetismo remanente o remanencia. Mediante vibraciones fuertes o calentamiento intenso se pueden desordenar, en parte o por completo, los imanes moleculares en los materiales magnéticamente duros y blandos.
2.5.3 EL CAMPO MAGNÉTICO.
El espacio en el que actúan fuerzas magnéticas se denomina campo magnético, este se forma, por ejemplo, entre los extremos de un imán recto o entre los brazos de un imán en forma de herradura.
Al igual que los campos eléctricos, también es posible visualizar los magnéticos. Por encima de un imán se coloca un papel tensado en marco y se esparcen sobre las limaduras de hierro, estas se ordenan, como consecuencia de la fuerza que actúa sobre ellas, formando líneas, por este motivo, se habla de las líneas de fuerza o del campo magnético. Hay que imaginarse el espacio alrededor del imán atravesado por las líneas de fuerza.
Se llama campo magnético a toda región del espacio en la cual una aguja imantada esta sometida a fuerzas magnéticas.
Un campo magnético se puede estudiar experimentalmente observando los efectos que produce sobre carga en movimiento. Al analizar los efectos del campo magnético sobre un flujo de electrones en un tubo de rayos catódicos
Cada corriente atómica es un pequeño circuito cerrado de dimensiones atómicas y puede, describirse apropiadamente como un dipolo magnético. El momento dipolar es la cantidad que interesa aquí, puesto que el campo de inducción magnética distante debido a un solo átomo se determina completamente especificando su momento dipolar magnético, . [2]
El momento magnético del i-ésimo átomo se expresa como . Se define una cantidad vectorial macroscópica, la magnetización , se suma vectorialmente, todos los momentos dipolares de un pequeño elemento de volumen y luego se divide el resultado por ; la cantidad resultante,
(2.4)
se llama momento dipolar magnético por unidad de volumen, o simplemente magnetización.
El haber tomado el límite en la ecuación (2.4) es el procedimiento acostumbrado de tomar los límites macroscópicos; se hace muy pequeño desde el punto de vista macroscópico, pero no tan pequeño que no contenga un número estadísticamente grande de átomos. La cantidad se vuelve entonces una función vectorial puntual. En el estado desmagnetizado, la suma dará cero como resultado de la orientación aleatoria de los , pero en presencia de un campo externo excitante, dependerá generalmente de este campo.
La función vectorial proporciona una descripción macroscópica de las corrientes atómicas interiores de la materia. Específicamente, mide el número de circuitos de corriente atómica por unidad de volumen multiplicado por el momento magnético efectivo o promedio de cada circuito. Desde el punto de vista puramente macroscópico, todos los efectos magnéticos debidos a la materia pueden describirse adecuadamente en función de , o por sus derivadas. Una de estas derivadas,, es la densidad de corriente de transporte equivalente que genera el mismo campo magnético que la magnetización ; ésta se llama densidad de corriente de magnetización JM. Antes de deducir esta importante relación que enlaza JM y ; un modelo simplificado de materia magnetizada como si ésta consistiese en corrientes atómicas que circulan en el mismo sentido por espiras o circuitos cerrados, lado a lado. Si la magnetización es uniforme, las corrientes en las diversas espiras tienden a eliminarse entre sí, y no hay corriente neta efectiva en el interior del material. Si la magnetización no es uniforme, la cancelación no es uniforme, la cancelación no será completa. Como ejemplo de magnetización no uniforme, es evidente que hay más carga moviéndose hacia abajo que moviéndose hacia arriba. Esto se denomina corriente de magnetización. Por lo tanto, aún cuando no haya transporte de carga, hay movimiento efectivo de carga hacia abajo, y esta corriente puede producir un campo magnético. [2]
La relación entre JM y . Se consideran dos elementos de pequeño volumen en un pedazo de material magnético, cada elemento de volumen colocado uno al lado del otro en la dirección del eje.
El potencial magnético puede determinarse a partir de las corrientes conocidas de la región de interés. Para las tres configuraciones estándar de corrientes las expresiones son las siguientes:
Filamento de corriente
Corriente de lámina
Corriente de volumen
POTENCIALES MAGNETICOS ESCALARES Y VECTORIALES.
La solución de problemas de campos electroestáticos resulta bastante simplificada con la utilización del potencial electroestático escalar . Aunque este potencial posee un significado físico muy real, matemáticamente no es más que un escalón que permite resolver un problema en varios pasos más pequeños. Dada una configuración de carga, primero se encuentra el potencial y entonces a partir de este la intensidad del campo eléctrico.
El potencial escalar magnético puede usarse para el cálculo del campo magnético causado ya sea por circuitos que conducen corriente o por capas dobles magnéticas (capas de dipolos). [4]
El potencial magnético escalar, el cual se designa como de cuyo gradiente se obtiene la intensidad de campo magnético (H),
El modelo atómico de la polarización de los materiales en un campo magnético es el de un electrón que se mueve en órbita alrededor de un núcleo positivo.
Un campo magnético interno se produce por la acción de los electrones que giran alrededor de sus propios ejes los cuales se mueven en órbita alrededor del núcleo.
Se llama campo magnético a toda región del espacio en la cual una aguja imantada esta sometida a fuerzas magnéticas.
La ciencia del magnetismo nació de la observación de que ciertas “piedras” (magnetitas) atraían pedazos de hierro. La palabra magnetismo viene de la región de magnesia en el Asia Menor, que es uno de los lugares en donde se encontraban esas piedras.
Este capítulo trata sobre campos magnéticos y las fuerzas que ejerce un campo magnético sobre las partículas cargadas, en los elementos de corriente y en las espiras o circuitos cerrados. Este estudio es importante para los problemas que se presentan en los aparatos eléctricos, por ejemplo, en los amperímetros, voltímetros, galvanómetros, entre otros.
Se presentarán conceptos de campo magnético, así como los conceptos de momentos magnéticos y fuerzas magnéticas.
De Wikipedia, la enciclopedia libre
Saltar a navegación, búsqueda
La inducción magnética o densidad de flujo magnético, cuyo símbolo es B, es el flujo magnético por unidad de área de una sección normal a la dirección del flujo, y en algunos textos modernos recibe el nombre de intensidad de campo magnético, ya que es el campo real.
La unidad de la densidad en el Sistema Internacional de Unidades es el tesla.

donde B es la densidad del flujo magnético generado por una carga que se mueve a una velocidad v a una distancia r de la carga, y ur es el vector unitario que une la carga con el punto donde se mide B (el punto r).

El campo inducción, B, o densidad de flujo magnético (los tres nombres son equivalentes) es más fundamental en electromagnetismo que el campo H, ya que es el responsable de las fuerzas en las cargas en movimiento y es, por tanto, el equivalente físico a E.
En física del magnetismo, la ley de Ampère, la cual se basó en una memoria de seis páginas de Hans Christian Oersted, relaciona un campo magnético estático con la causa que la produce, es decir, una corriente eléctrica estacionaria. Es análoga a ley de Gauss.
Σ BIIΔ l = μ0 ΣI
de donde:
ΣI es la corriente neta, Δl es la distancia recorrida, BII el campo magnético generado y Σ BII Δl es la suma de ambos, además de que μ0 es igual a 4 π x 10-7 T (teslas) x metro/ A (amperes) (T x m/A), la constante de permeabilidad en el vacío, de aquel campo será B= μ0 I/ 2πr
Forma integral Dada una superficie abierta S por la que atraviesa una corriente eléctrica I, y dada la curva C, curva contorno de la superficie S, la forma original de la ley de Ampère para medios materiales es:

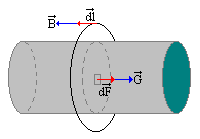
Ley de Biot - Savart
El campo magnético H en las proximidades de un elemento de corriente eléctrica es:
- Directamente proporcional al valor de la densidad de corriente que circula por el hilo, G.
- Inversamente proporcional a la distancia del punto considerado al hilo conductor, r.
En general:
dH = -(1/4p ){G x (1/r3)r}dv
La expresión anterior recibe el nombre de Ley de Biot-Savart, que es la ley del campo magnético, equivalente a la ley de Coulomb para el campo eléctrico.
La expresión que determina la forma de H alrededor del cable conductor es:
H = 1/4p ò ò ò v{-G x (1/r3)r}dv
Ecuación de la continuidad
Imagínese a dos electrodos inmersos en un medio conductor ideal que están a potenciales diferentes medidos respecto a tierra.
El electrodo 1 se encuentra a un potencial más elevado que el electrodo 2. k es la conductividad del medio por el que fluye la corriente I. La superficie cerrada F encierra al electrodo 1 y, por lo tanto, es atravesada por la corriente I. La corriente atraviesa al medio conductor con una densidad G y así mismo a cualquier superficie que encierre al electrodo 1.
(5)
Experimentalmente puede observarse que la carga eléctrica del electrodo 1 disminuye en función del tiempo, como era de esperarse según la ley de la conservación de la carga, que reza que la carga no se crea ni se destruye.
I = - Dt Q (6)
donde Q es la carga espacial encerrada por la superficie F
Q = ò ò ò v r dv (7)
y r es la densidad de carga espacial.
Con el teorema de Gauss se obtiene la siguiente expresión:
= ò ò ò v divG dv (8)
con las ecuaciones (6), (7) y (8) se llega a la ecuación de la continuidad
div G + Dt r = 0
Esta ecuación comprueba la existencia de las corrientes de desplazamiento.

corriente que entra. · corriente que sale.
Con (1) se obtiene que rot H = 0, por lo tanto el campo magnético puede expresarse como el gradiente de un potencial escalar magnético:
H = -grad Vm
Como el campo magnético no tiene fuentes:
div B = 0 Þ m div (-grad Vm) = 0 Ù \ div grad Vm = 0
D Vm = 0 (4)
esta es la ecuación de Laplace del campo magnético libre de densidades de corriente.
Es preciso resaltar la analogía que se puede establecer entre el campo magnético y el campo eléctrico para observar la dualidad de sus ecuaciones:
CAMPO ELÉCTRICO
CAMPO MAGNÉTICO
rot E = 0
E = -grad V
rot H = 0 Þ H = -grad Vm
Densidad
D = e E
Inducción o Densidad
B = m H
Constante dieléctrica del vació
en el vacío e 0 = 8,85 X 10-12 C/Nm2
Permeabilidad magnética del vacío
en el vacío m 0 = 4p · 10-7 Tm/A
Constante dieléctrica
e = e 0 e r
Permeabilidad magnética
m = m 0 m r
Flujo eléctrico
y e = ò ò D . dF
Flujo magnético
y m = ò ò B . dF
I = ò ò G.dF
La ley de Ampere puede escribirse como:
Por lo tanto
Con el teorema de Stokes se puede deducir que
por lo tanto
rot H = G (1)
Todo esto indica que en cada espacio donde existan densidades de corriente existen también rotacionales o remolinos del campo magnético.
Basándose en estas observaciones, es válido decir que no existen cargas magnéticas, pues, el campo magnético es generado por dipolos magnéticos y por lo tanto, su divergencia es nula.
div H = 0
por ser la inducción magnética un vector linealmente dependiente del campo magnético su divergencia también es nula:
div B = 0
El Potencial Vectorial Magnético libre de fuentes "A"
Dado que la divergencia del campo magnético es nula, es decir, el campo magnético no tiene fuentes, entonces, este se puede expresar como el rotacional de un campo vectorial libre de fuentes, en otras palabras, como el rotacional de un campo no gradiental.
div B = 0 Þ B = rot A Ù div A = 0 (2)
con (1):
G = rot H Þ m G = rot B
Con (2):
mG = rot rot A Þ mG = -D A (3)
El Potencial Escalar Magnético "Vm"
Supóngase el caso en el que el campo magnético es generado por la corriente que fluye a través de un inductor de espiras muy finas. El volumen encerrado por el inductor no contiene densidades de corriente, por lo tanto G = 0.
B = m H
H es el campo magnético.
Una manera de demostrar lo anteriormente dicho es haciendo el siguiente análisis:
Ley de Ampere
Ampere formuló la idea de que las propiedades magnéticas de los materiales denominados imanes eran debidas a pequeñas corrientes eléctricas que existían en dichos materiales.
Hoy día se sabe que los electrones de los átomos presentan dos momentos magnéticos debidos a ser una carga eléctrica en movimiento; estos momentos son el magnético de espín y el magnético orbital (debido al movimiento orbital de los electrones).
En general, el valor del campo magnético en las proximidades de un imán o de una corriente eléctrica depende del medio material que rodee al conductor o al imán, debido a la interacción de los momentos magnéticos de los electrones de los átomos del material.
En la actualidad, la relación cuantitativa entre la corriente "I" y la inducción magnética "B" se representa de la siguiente manera:

De las experiencias indicadas es fácil deducir que una corriente eléctrica se comporta como un imán, o expresándolo de otra forma, se puede decir que una corriente eléctrica crea en sus proximidades un campo magnético, entendido este campo como zona en la que se manifiestan efectos magnéticos.
Como la corriente eléctrica es un flujo de cargas eléctricas, entonces, puede afirmarse que el campo magnético no sólo es generado por imanes sino también por la presencia de cargas eléctricas en movimiento ordenado, es decir, por densidades de corriente.
Entonces, puede definirse al campo magnético como la modificación del espacio debido a la presencia de imanes o densidades de corriente.
Si por el momento se consideran a los alambres que transportan corrientes como las fuentes típicas de campos magnéticos y como los objetos típicos sobre los cuales pueden actuar los campos magnéticos, entonces, es posible sugerir que las corrientes generan campos magnéticos y que los campos magnéticos ejercen fuerzas sobre las corrientes.
CAMPO MAGNETOSTATICO
PRINCIPIOS DE LA MAGNETOSTÁTICA Y LA ELECTRODINÁMICA
El magnetismo es una propiedad de la materia que se manifiesta por unas fuerzas de atracción y repulsión. Esta propiedad se pone de manifiesto con determinados minerales, como la magnetita (mineral de hierro). Los imanes permanentes son barras construidas con minerales naturales o con aleaciones especiales de hierro, cobalto y níquel.
Las propiedades que se observan en los imanes son:
- Todos los imanes poseen dos polos o regiones próximas a sus extremos en las que se concentra la actividad magnética.
- Existen dos tipos de polos magnéticos: uno de ellos se denomina polo norte y el otro se denomina polo sur.
- Los imanes se orientan libremente en la Tierra, de forma que uno de sus polos se orienta siempre hacia el polo norte geográfico (este polo es el que se denomina polo norte magnético). En esta propiedad se basa la utilización de la brújula como instrumento de orientación. De lo anterior se puede deducir que la Tierra se comporta como un imán.
- Polos de idéntico nombre se repelen y polos de distinto nombre se atraen.
- Existen materiales, como el hierro dulce, que son atraídos siempre por cualquiera de los polos de un imán. Este tipo de sustancias se dice que están desimantadas.
- No se han observado nunca polos magnéticos aislados.
La magnetostática es la parte de la física que estudia los fenómenos relativos a los imanes y al campo magnético creado por éstos, así como el comportamiento de los diferentes materiales sometidos a la acción de dicho campo.
Experiencia de Oersted
En 1820 el físico danés Hans Christian Oersted observó que una aguja magnética o brújula se orientaba en una determinada dirección en las proximidades de un hilo por el que circulaba corriente eléctrica.
La orientación que adquiría la brújula era tal que dependía de la dirección de la corriente eléctrica por el hilo conductor. Esta orientación es siempre perpendicular a la dirección de la corriente eléctrica, y el polo norte de la brújula se orienta en la dirección de los dedos extendidos de la mano derecha, cuando el dedo pulgar está extendido en la dirección de la corriente eléctrica.
viernes, 16 de octubre de 2009
TRABAJO EN CLASES...TERCERA UNIDAD
E=F/Q .18/(6X10)-6 C.= 30000N/C
F= ((5X10)20N/C.)(1.6X10^19) =80N
Q=12/3X10^6=4X10^6
LA INTENSIDAD DE CORRIENTE ELECTRICA QUE CIRCULA POR UN CONDUCTOR ES DIRECTAMENTE PROPORCIONAL AL VOLTAJE APLICADO A SUS ESTREMOS E INVERSAMENTE PROPORCIONAL A SU RESISTENCIA.
I=V/R
V=RI
R=V/I
A) .-ENCUENTRA LA FUERZA ELECTROSTATICA EJERCIDA POR UN PROTON SOBRE OTRO.
B).-COMO SE COMPARA LA MAGNITUD DE ESTA FUERZA CON LA MAGNITUD DE LA FUERZA GRAVITACIONAL ENTRE DOS PROTONES.
C).-CUAL DEBE SE LA RAZON ENTRE LA CARGA Y LA MASA DE UNA PARTICULA ES IGUAL A LA MAGNITUD DE LA FUERZA ELECTROSTATICA ENTRE ELLAS
FE=(9X10^9)(1.6X10^-19)(1.6X10^-19)/ (3.80X10^-10)2=1.59X10^-9
FG=(6.7X10^-11)( 1.67X10^-27) (1.67X10^-27)/ (3.80X10^-10)2=1.23X10^-45 N
FE21=(9X10^9) (7X10^-6) (2X10^-6) / (.5)^2= .50344
FE23=(9X10^9) (7X10^6) (4X10^-6)=1.068
FE13=(9X10^9) (4X10^-6) (2X10^-6)=.2876
FX=-F13 + F23= .7192
FY=.50344
LAS DIMENSIONES DEL RECTANGULO SON L=60 CM Y W=15.
CALCULE LA MAGNITUD Y DIRECCION DE LA FUERZA ELECTRICA NETA EJERCIDA SOBRE LA CARGA EN LA ESQUINA IZQUIERDA INFERIOR POR LAS OTRAS 3 CARGAS.
F1,3= ((9X10^9) (10X10^-6))^2 / (.15)^2=40 N
F2,3= ((9X10^9) (10X10^-6))^2 / (.61)^2=2.41 N
FT= 2.5-2.41-40= 44.91 N
H= RAIZ CUADRADA DE .6^2 MAS .15^2=.61m
viernes, 9 de octubre de 2009
UNIDAD II- CAMPOS ELECTROSTATICOS EN EL ESPACIO MATERIAL

Al aplicar un campo externo, los electrones de valencia se mueven hasta llegar al equilibrio


Fα = q/r²
F/r² = 40N (2)² = 40/4= 10N
E = F/q
F= Magnitud del campo de fuerza "N"q= Carga de prueba "c"E= Magnitud del campo electrico "N/c"
La magnitud del campo electrico producido por una carga puntual que a una distancia d, de ella se obtiene con la formula:
E = K q/d²
E= Campo electrico "N/c"q= Carga electrica "c"d= Distancia "m"K= 9x109 N.m²/c²
Una carga de 5x10-6 c se introduce a una región donde actúa un campo de fuerza de 0.04 N. ¿Cuál es la intensidad del campo electrico en esa región?
E= k q/d²
E= F / q
E= 0.04 / 5x10-6
E= 8000 N/c
La magnitud del campo producido por una carga de 4x10-9 c a una distancia de 30 cm de su centro es?
k= 9x109 E= 9x109 (4x10)-9 / (o.3)²d= 0.3m
TaReA...
A= 2i - 3j - k y B= i + 4j - 2k
hallar:
a) A x B
b) A . B
c) A + B
d) A - B
e) B x A
jueves, 8 de octubre de 2009

Vα= 15 m/s Δx= VoΔt xo= 0 a= 3 m/s⌃2 xα= 0 to= 0Δx=? to= 0 Vo= 0
vf=? Vf-Vp=?
*PARA EL AUTO
Δx= xa - Xo = xa
xa=xp
tp= 2(15)/3
t= 10 seg.*
xa=xp= 15(10)
xa= 150 mts.
*VELOCIDAD
a =ΔV/Δt => ap=Vp/tp
por lo tanto
Vp=aptp= (3)(10)=
Vp= 30 mts.
PROBLEMAS EN CLASE

BY= Bsen37º= 10.8326 m
AX= -12 m
Ay= θ
use el metodo de componentes para obtener la magnitud y dirección de :
B) La suma vectorial B+A
C) La diferencia vectorial A-B
D) La diferencia vectorial B-A
A) -(-12 m + 14.37 m ) + ( 10.38)
Fx= 2.37 m Fy= 10.38 m
B) 14.37 + (-12 m ) Fy= 10.8326 + 0
Fx= 2.37 m Fy= 10.8326
C) -12 m -18 m = -30m
D) 18 - (-12) = 30 m
x=r cosө y=r senө z=z



Δr2= (2.3i - 1.4j - 3.6k) cm
Δr3= (-1.3i + 1.5 j ) cm

A= 2.00i + 3.00 j y B= 5.00i - 4.00j
i= 2.00 + 5.00 = 7.00i
j= 3.00 - 4.00 = -1.00j



















